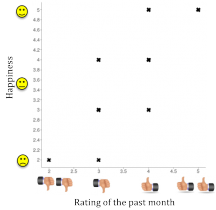
Figure 3-1: Scatterplot of the association between happiness and ratings of the past month, a positive correlation (r = .81). Each dot represents an individual.
In correlational research we are interested in how two variables are related: How does change in one variable relate to change in another?
Here, we do not intervene and change behaviour, as we do in experiments. In correlational research we see patterns that go together, but we usually cannot infer what causes what. In addition, with correlational research you can examine only two variables at a time, no more and no less.
Consider the following example. Researchers used a correlational design to test whether spending on others is related to happiness (Dunn, Aknin, & Norton, 2008). The researchers asked people how much of their income they spend on others or donate to charity, and then asked them how happy they are. As you might suspect, these two variables were related, but perhaps not in the way you predicted. The more money people spent on others, the happier they were!
To find out how well two variables go together, we can plot the relation between the two scores on what is known as a scatterplot. A scatterplot is a powerful data visualization tool. It uses X and Y coordinates to display the values of the two variables in our data set.
In Figure 3-1, each dot in the scatterplot represents a data point (in this case it is individuals, but it could be some other unit). Importantly, each dot provides us with two pieces of information—in this case, information about how good the person rated the past month (x-axis) and how happy the person felt in the past month (y-axis). Which variable goes on which axis does not matter. According to Figure 3-1, people are happier when they perceive the month is good as opposed to bad.
The association between two variables can be represented using the scatterplot or summarized statistically using the correlation coefficient (abbreviated asr). A correlation coefficient tells us information about the direction and strength of the association between two variables. For the example above, the direction of the association is positive. That means that people who perceived the past month as being good reported feeling happy, whereas people who perceived the month as being bad reported feeling less happy.
With a positive correlation, the two variables go up together and go down together. In a scatterplot, the dots form a pattern that extends from the bottom left to the upper right. The r value for a positive correlation is positive (usually the positive sign is omitted). Here, the r value is .81.

Figure 3-2: Scatterplot showing the association between average male height and pathogen prevalence, a negative correlation (r = –.83). Each dot represents a country. (Chiao, 2009)
A negative correlation is one in which the two variables move in opposite directions. That is, as one variable goes up, the other one goes down. Figure 3-2 shows the association between average height of males in a country and pathogen prevalence (or commonness of disease) of the country. In this scatterplot, each dot represents a country. Notice how the dots extend from the top left to the bottom right. What does this mean in real world terms? It means that people are shorter in parts of the world where there is more disease. Thervalue for a negative correlation is negative, that is, it has a minus (–) sign in front of it. Here it is –.83.
The strength of a correlation has to do with how well the two variables go together. Recall that in Professor Dunn’s correlational study, spending on others was positively correlated with happiness. The more people spent on others, the happier they were. At this point, you may be thinking to yourself, I know a very generous person who gave away lots of money to other people but is miserable! Or maybe you know of a very stingy person who is happy as can be.
Yes, there might be exceptions. If an association has a lot of exceptions, it is a weak correlation. If an association has few or no exceptions, then it is a stronger correlation. A strong correlation is one in which the two variables always or almost always go together. In the case of happiness and how good the week is, the association is strong. The stronger a correlation is, the tighter the dots in the scatterplot will be arranged along a sloped line.
The r value of a strong correlation will have a high absolute value. In other words, you disregard whether there is a negative sign in front of the r value, and just consider the size of the numerical value. If the absolute value is large, it is a strong correlation. A weak correlation is one in which the two variables go together some of the time, but not all of the time. Figure 3-3 shows the relation between valuing happiness and grade point average (GPA). People who value happiness more tended to earn slightly lower grades, but there were lots of exceptions to this. The r value for a weak correlation will have a low absolute value. If two variables are so weakly related as to be unrelated, we say they are uncorrelated, and the r value will be zero or very close to zero. Is the correlation between pathogen prevalence and height strong? Compared to Figure 3-3, the dots in Figure 3-2 are tighter and less dispersed. The absolute value of –.83 is large. Therefore, this is a strong negative correlation. Table 1-1 states guidelines around how to interpret the strength of a correlation based on the value of the correlation coefficient.
Table 3-1
|
‘Value of the Correlation Coefficient’
|
|
1
|
Perfect
|
|
0.7 – 0.9
|
Strong
|
|
0.4 – 0.6
|
Moderate
|
|
0.1 – 0.3
|
Weak
|
|
0
|
Zero
|
Can you guess the strength and direction of the correlation between age and year of birth? If you said this is a strong negative correlation, you are correct! Older people will always have lower years of birth than younger people. In fact, this is a perfect correlation because there are no exceptions to this pattern.

Figure 3-3: Scatterplot showing the association between valuing happiness and GPA, a weak negative correlation (r = –.32). Each dot represents an individual.
Correlation Does Not Imply Causation
If generosity and happiness are positively correlated, does that mean that being generous causes happiness? Similarly, if pathogen prevalence and height are negative correlated, does disease cause people to grow short? From the correlation alone, we can’t tell. In the first case, it may be that happiness causes generosity or that generosity causes happiness. Or even a third variable might be causing both happiness and generosity, creating a spurious link between the two. For example, wealth could be the third variable that both causes greater happiness and causes greater generosity. This is why the correlation is not used to determine causality.
To browse through a number of amusing examples of spurious correlations, visit the website: http://www.tylervigen.com/
Share your favourite example on the micro-blog discussion forum Microblog for IRMP102 or on Twitter (using the hashtag #OERuIRMP102).
In correlational research we are interested in how two variables are related: How does change in one variable relate to change in another?
Here, we do not intervene and change behaviour, as we do in experiments. In correlational research we see patterns that go together, but we usually cannot infer what causes what. In addition, with correlational research you can examine only two variables at a time, no more and no less.
Consider the following example. Researchers used a correlational design to test whether spending on others is related to happiness (Dunn, Aknin, & Norton, 2008). The researchers asked people how much of their income they spend on others or donate to charity, and then asked them how happy they are. As you might suspect, these two variables were related, but perhaps not in the way you predicted. The more money people spent on others, the happier they were!
To find out how well two variables go together, we can plot the relation between the two scores on what is known as a scatterplot. A scatterplot is a powerful data visualization tool. It uses X and Y coordinates to display the values of the two variables in our data set.
In Figure 3-1, each dot in the scatterplot represents a data point (in this case it is individuals, but it could be some other unit). Importantly, each dot provides us with two pieces of information—in this case, information about how good the person rated the past month (x-axis) and how happy the person felt in the past month (y-axis). Which variable goes on which axis does not matter. According to Figure 3-1, people are happier when they perceive the month is good as opposed to bad.
The association between two variables can be represented using the scatterplot or summarized statistically using the correlation coefficient (abbreviated asr). A correlation coefficient tells us information about the direction and strength of the association between two variables. For the example above, the direction of the association is positive. That means that people who perceived the past month as being good reported feeling happy, whereas people who perceived the month as being bad reported feeling less happy.
With a positive correlation, the two variables go up together and go down together. In a scatterplot, the dots form a pattern that extends from the bottom left to the upper right. The r value for a positive correlation is positive (usually the positive sign is omitted). Here, the r value is .81.
A negative correlation is one in which the two variables move in opposite directions. That is, as one variable goes up, the other one goes down. Figure 3-2 shows the association between average height of males in a country and pathogen prevalence (or commonness of disease) of the country. In this scatterplot, each dot represents a country. Notice how the dots extend from the top left to the bottom right. What does this mean in real world terms? It means that people are shorter in parts of the world where there is more disease. Thervalue for a negative correlation is negative, that is, it has a minus (–) sign in front of it. Here it is –.83.
The strength of a correlation has to do with how well the two variables go together. Recall that in Professor Dunn’s correlational study, spending on others was positively correlated with happiness. The more people spent on others, the happier they were. At this point, you may be thinking to yourself, I know a very generous person who gave away lots of money to other people but is miserable! Or maybe you know of a very stingy person who is happy as can be.
Yes, there might be exceptions. If an association has a lot of exceptions, it is a weak correlation. If an association has few or no exceptions, then it is a stronger correlation. A strong correlation is one in which the two variables always or almost always go together. In the case of happiness and how good the week is, the association is strong. The stronger a correlation is, the tighter the dots in the scatterplot will be arranged along a sloped line.
The r value of a strong correlation will have a high absolute value. In other words, you disregard whether there is a negative sign in front of the r value, and just consider the size of the numerical value. If the absolute value is large, it is a strong correlation. A weak correlation is one in which the two variables go together some of the time, but not all of the time. Figure 3-3 shows the relation between valuing happiness and grade point average (GPA). People who value happiness more tended to earn slightly lower grades, but there were lots of exceptions to this. The r value for a weak correlation will have a low absolute value. If two variables are so weakly related as to be unrelated, we say they are uncorrelated, and the r value will be zero or very close to zero. Is the correlation between pathogen prevalence and height strong? Compared to Figure 3-3, the dots in Figure 3-2 are tighter and less dispersed. The absolute value of –.83 is large. Therefore, this is a strong negative correlation. Table 1-1 states guidelines around how to interpret the strength of a correlation based on the value of the correlation coefficient.
Table 3-1
‘Value of the Correlation Coefficient’
1
Perfect
0.7 – 0.9
Strong
0.4 – 0.6
Moderate
0.1 – 0.3
Weak
0
Zero
Can you guess the strength and direction of the correlation between age and year of birth? If you said this is a strong negative correlation, you are correct! Older people will always have lower years of birth than younger people. In fact, this is a perfect correlation because there are no exceptions to this pattern.
Activity
Visit the “Interpreting Correlations” website and use the interactive tool to depict correlations ranging from -1 to +1
Correlation Does Not Imply Causation
If generosity and happiness are positively correlated, does that mean that being generous causes happiness? Similarly, if pathogen prevalence and height are negative correlated, does disease cause people to grow short? From the correlation alone, we can’t tell. In the first case, it may be that happiness causes generosity or that generosity causes happiness. Or even a third variable might be causing both happiness and generosity, creating a spurious link between the two. For example, wealth could be the third variable that both causes greater happiness and causes greater generosity. This is why the correlation is not used to determine causality.
Activity
To browse through a number of amusing examples of spurious correlations, visit the website: http://www.tylervigen.com/
Share your favourite example on the micro-blog discussion forum Microblog for IRMP102 or on Twitter (using the hashtag #OERuIRMP102).
Activity
Visit the “Everyday Research Methods” blog and browse through a few examples of reports of correlational studies. Note how sometimes the same research is described differently by the researchers and journalists.
Content is available under the
Creative Commons Attribution Share Alike License.
Privacy Policy | Authors